FDP Heikendorf fordert weiter die Abschaffung der Tourismusabgabe: „Ein Bürokratiemonster ohne echten Nutzen“

Die FDP-Fraktion in der Gemeindevertretung Heikendorf fordert nach wie vor die vollständige Abschaffung der Tourismusabgabe. Der entsprechende Antrag wurde gestellt, fand aber leider keine Mehrheit.
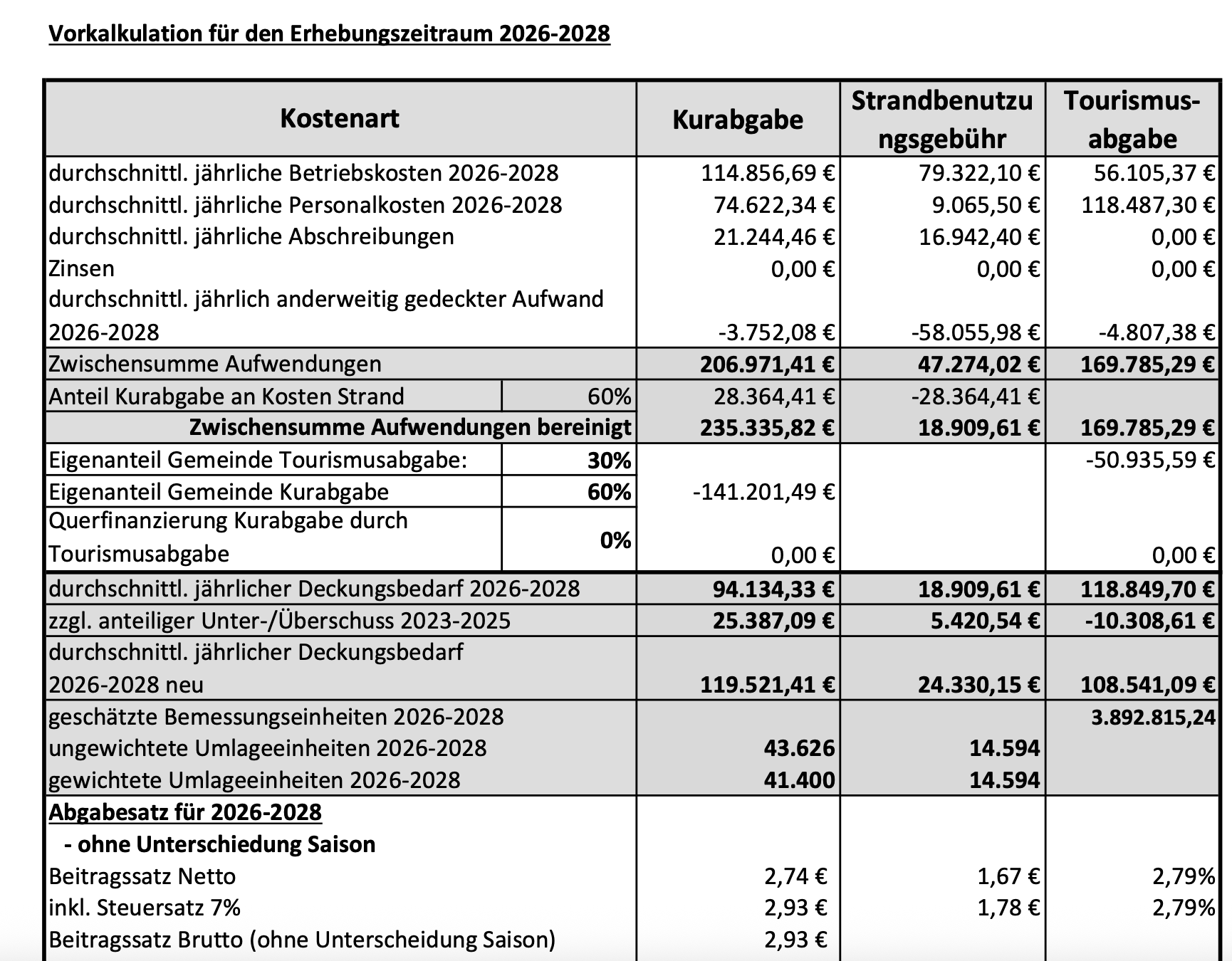
Hintergrund ist die neue Kalkulation für den Zeitraum 2026–2028, die deutlich zeigt, dass sich die Abgabe wirtschaftlich nicht lohnt und vor allem Verwaltung bindet (siehe Bild im Anhang).
„Die Tourismusabgabe ist ein echtes Bürokratiemonster“, sagt Gunnar Schulz, Fraktionsvorsitzender der FDP Heikendorf. „Sie belastet nicht nur unsere örtlichen Unternehmen mit unnötiger Papierarbeit, sondern bindet auch wertvolle Verwaltungskapazitäten. Wenn wir diese Abgabe abschaffen, können Mitarbeiterinnen und Mitarbeiter im Amt Schrevenborn endlich wieder sinnvollere Aufgaben übernehmen – zum Beispiel in Bereichen, die tatsächlich der Gemeinde und den Bürgern zugutekommen.“
Die Abgabe deckt nicht einmal die Verwaltungskosten, die sie selbst verursacht.
„Die Zahlen sprechen eine klare Sprache – die Tourismusabgabe ist ein Nullsummenspiel. In Wahrheit bleibt für den Tourismus praktisch nichts übrig, weil das Geld sofort wieder in Verwaltungsaufwand verschwindet“, so Schulz.
Hinzu kommt: Heikendorf ist als Fehlbedarfsgemeinde auf Zuschüsse des Landes angewiesen. Das Innenministerium droht jedoch mit Kürzungen, wenn nicht alle potenziellen Einnahmequellen ausgeschöpft werden.
„Dass das Land einer Gemeinde Zuwendungen streicht, nur weil sie auf eine ineffiziente Abgabe verzichten will, ist absurd“, kritisiert Schulz. „Wenn eine Abgabe kaum oder gar keinen Ertrag bringt, aber Verwaltung und Wirtschaft belastet, kann das doch nicht der Ernst des Innenministeriums sein. Über diese Praxis muss man auch im Land endlich nachdenken.“
„Unser Ziel ist klar: weniger Bürokratie, mehr Freiheit für die Wirtschaft und eine effiziente Verwaltung. Heikendorf braucht keinen bürokratischen Moloch, sondern gesunden Menschenverstand“, fasst Schulz zusammen.